Valor actual neto: función financiera
VNA
DEFINICIÓN
Contenidos
Esta función de Excel calcula el valor actual neto de los flujos de caja futuros regulares o periódicos esperados de un activo o de un proyecto de inversión. Toda ello calculado a partir de un tipo de descuento determinado. Si los flujos de caja no fueran periódicos utilizaremos otra función diferente que se verá próximamente.
SINTAXIS
=VNA(tasa;valor1;valor2;valor3;…) |
En esta función nos encontramos que todos los argumentos son obligatorios.
OBLIGATORIOS:
tasa |
Representa el tipo de descuento o tipo de interés exigido por la empresa para la realización del cálculo. Debe venir expresada en la misma unidad de tiempo que la periodicidad con la que produzcan los correspondientes flujos. |
|
valor1,valor2;valor3;… |
Son los distintos argumentos que representan los sucesivos futuros pagos y cobros de la inversión |
|
ACLARACIONES
-
- Si el primer flujo de caja se produjera al principio del primer período, este valor se deberá añadir al resultado del Valor actual neto, es decir, no tendríamos que incluirlo en los argumentos valores.
-
- Os habréis dado cuenta que esta función es muy similar a la función VA (valor actual) que ya explicamos. La diferencia principal con ésta es que la función VA ya vista permite que los flujos de caja sean pospagables o prepagables. Además estos flujos de caja en VA han de ser constantes y en cambio en esta función los flujos van teniendo distintos valores y no tienen que ser constante.
- Esta función también tiene una gran relación con la función TIR (tasa interna de retorno) explicada en la anterior entrada, ya que por definición TIR podemos decir que es el tipo de interés que hace CERO precisamente al VNA (valor actual neto).
FUNDAMENTOS DE MATEMÁTICA FINANCIERA
Una inversión será:
- Realizable cuando el VNA sea mayor que cero.
- Indiferente cuando el VNA sea igual a cero.
- Inviable cuando el VNA sea inferior o menor que cero.
El planteamiento en matemáticas financieras para el cálculo del VAN sería:
Donde Co es el desembolso inicial de la inversión; F1, F2, F3, …,Fn los sucesivos flujos de efectivo esperados de la inversión y “i” el tipo de interés de descuento aplicado en los cálculos.
SUPUESTOS PRÁCTICOS DE APLICACIÓN
SUPUESTO Nº 1
Una empresa se dedica a la venta de motocicletas de baja cilindrada y está pensando la posibilidad de ampliar su negocio hacia la venta de complementos utilizados diariamente para el disfrute de las motocicletas.
Realizado un estudio, ha previsto un desembolso de 600.000 euros en el momento inicial y los siguientes cobros y pagos que se generarían durante la vida de la inversión, que es de 4 años:
|
AÑOS |
COBROS |
PAGOS |
|
1 |
100.000 |
50.000 |
|
2 |
200.000 |
60.000 |
|
3 |
300.000 |
65.000 |
|
4 |
300.000 |
65.000 |
¿Cuál es el valor actual neto de cada una de las inversiones?
En base al resultado obtenido, ¿cuál sería el proyecto que debería escoger la empresa teniendo en cuenta este criterio de selección de inversiones?.
SUPUESTO Nº 2
A un inversor se le presentan las siguientes posibilidades para realizar una determinada inversión:
|
DESEMBOLSO INICIAL |
FLUJO 1 |
FLUJO 2 |
FLUJO 3 |
FLUJO 4 |
FLUJO 5 |
|
| PROYECTO A |
1.000.000 |
100.000 |
150.000 |
200.000 |
250.000 |
300.000 |
| PROYECTO B |
1.500.000 |
200.000 |
300.000 |
350.000 |
400.000 |
500.000 |
| PROYECTO C |
1.700.000 |
400.000 |
600.000 |
300.000 |
600.000 |
400.000 |
Debemos calcular el proyecto más rentable según el criterio del Valor Actual Neto y suponiendo una tasa de actualización o descuento del 7 %.
SUPUESTO Nº 3
Un inversor compra un activo financiero por 10.369,73 euros. Los flujos de caja netos que recibirá este inversor serán los siguientes:
36 cuotas mensuales de: 66,17 euros.
Una última cuota (la número 37) de: 10.613.85 euros.
Determina el VAN de este activo financiero, para una tasa de descuento del 8,1487 % anual, utilizando la función VNA.
SOLUCIONES
Puedes ver las soluciones a los supuestos prácticos en la hoja de cálculo que puedes bajar en el siguiente enlace. Puedes hacer distintas simulaciones cambiando los parámetros y adaptando los supuestos prácticos a tus necesidades, desprotegiendo la hoja.
Próxima entrada función TIR.NO.PER (Tasa interna de retorno no periódica)
Puedes suscribirte al blog y recibir nuevos posts similares a este conforme se vayan publicando, en el formulario situado al final del post.
Saludos cordiales
Luis Manuel Sánchez


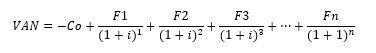


1 comentario en «FINANCIERAS EXCEL: la función VNA (valor actual neto)»